rosefert.blogg.se

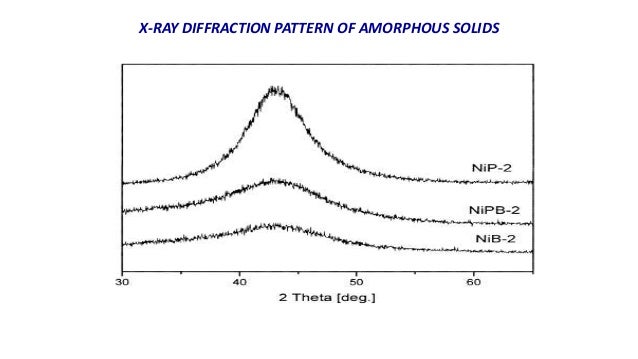
The use of XRD in pharmaceutical research is extensively increasing due to its wide application. Interference and diffraction effects operate simultaneously and generally produce minima at different angles. X-ray diffraction (XRD) is used for the primary characterization of material properties like crystal structure, crystallite size, and strain. If both equations are used simultaneously, it is good practice to use a different variable (such as n) for one of these integers in order to keep them distinct. Fluctuations of atoms about the ideal lattice positions that preserve the long-range order of the lattice only give rise to the Debye-Waller factor, which reduces peak heights but does not broaden them. Equation 4.1 also uses m, but this time to refer to diffraction minima. Another alternative expression for the diffraction conduction can be given in terms of Lauer equations. The finite size of a crystal is not the only possible reason for broadened peaks in X-ray diffraction. Τ = K λ β cos ⁡ θ Peak broadening due to disorder of the second kind Simple models give the geometry of the intensities in a diffraction pattern, but higher level. This function is virtually zero except at the points where x n ( n is an integer. Unlike x-ray diffraction and neutron diffraction where the simplest approximations are quite accurate, with electron diffraction this is not the case. My textbook, Solid-State Physics, Fluidics, and Analytical Techniques in Micro- and Nanotechnology, by Madou, says the following in a section on X-Ray Intensity and Structure Factor F ( h k l): In Figure 2.28 we have plotted y sin 2 ( M x) sin 2 ( x). It is used in the determination of size of crystals in the form of powder. These involve more general analyses using relativistically corrected Schrdinger equation methods. It is often referred to, incorrectly, as a formula for particle size measurement or analysis. The equations must be satisfied simultaneously, it is in general difficult to produce a diffracted beam with a fixed wavelength and a fixed crystal.

They are named after physicist Max von Laue (1879–1960).The Scherrer equation, in X-ray diffraction and crystallography, is a formula that relates the size of sub- micrometre crystallites in a solid to the broadening of a peak in a diffraction pattern.

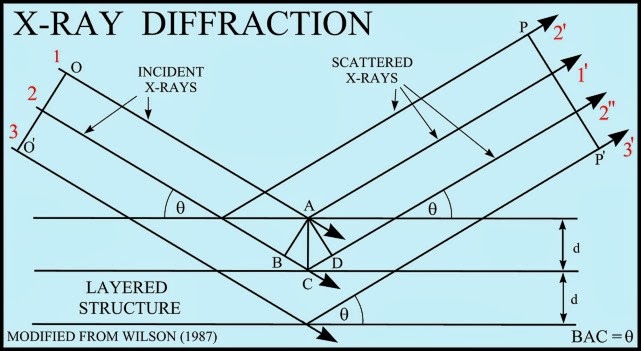
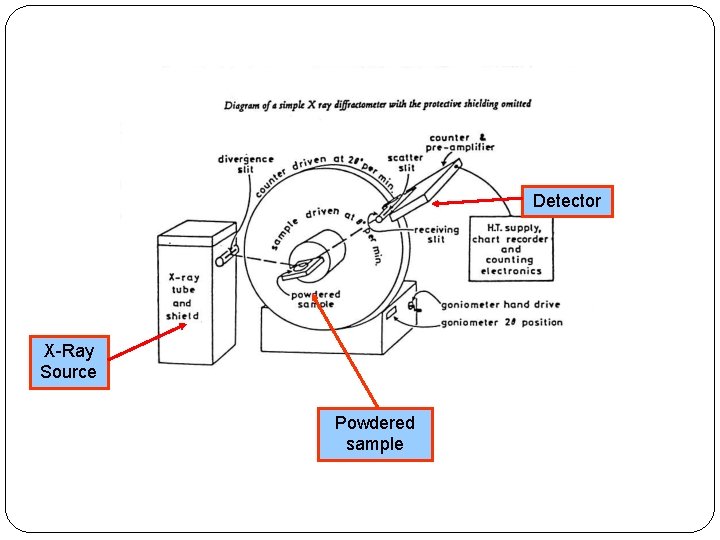
X-ray diffractometers are not used to identify the physical properties of which of the following a) Metals. To obtain nearly monochromatic x-rays, an x-ray tube is used to produce characteristic x-rays. A basic instrument for such study is the Bragg spectrometer. In crystallography and solid state physics, the Laue equations relate incoming waves to outgoing waves in the process of elastic scattering, where the photon energy or light temporal frequency does not change upon scattering by a crystal lattice. This set of Analytical Instrumentation Multiple Choice Questions & Answers (MCQs) focuses on X-Ray Diffractometers. Much of our knowledge about crystal structure and the structure of molecules as complex as DNA in crystalline form comes from the use of x-rays in x-ray diffraction studies. Wulff suggested to consider the rays reflected from the crystal. Equations describing diffraction in a crystal lattice Laue equation In the abovementioned Laue method, diffraction of X-rays passing through the crystal is observed.W.H.